English scholar and mathematician John Horton Conway, Ph.D., produced significant and long-standing contributions to mathematics in a range of fields — from game theory and coding theory to algebra, number theory, and knot theory.
Dr. Conway made mathematics accessible, and his love of games, coupled with his curiosity and creativity, sparked an enthusiasm in others, even among those for whom math was not a first love. The retired Princeton University professor, 82, died of complications of COVID-19 in April.
One of his long-standing contributions was to the field of knot theory, a subspecialty of a field of mathematics known as topology — the study of objects’ undisputable geometric properties and the nature of spaces and how these shapes are possible. It is useful for understanding DNA and protein folding.
In mathematics, knots are known to be a closed, non-self-intersecting curve embedded in three dimensions. They cannot be untangled to produce a simple loop. Dr. Conway, then at Princeton, invented a system of notation for tabulating knots, now known as Conway notation, while extending the knot tables to 11 crossings.
And that is where it ended.
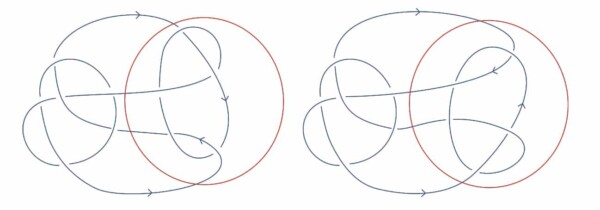
Questions arose whether the Conway knot is a slice of a higher-dimensional knot.
Whether something is slice is one of the first questions knot theorists ask about knots in higher dimensions. Slice means the knot is a cross section of a four-dimensional shape, while not slice means it cannot be cut from a four-dimensional shape.
Thinking outside the knot
Though many mathematicians suspected that the knot was not slice, they were not able to prove it. What has been coined the Conway knot remained an unresolved issue within knot theory for 50 years.
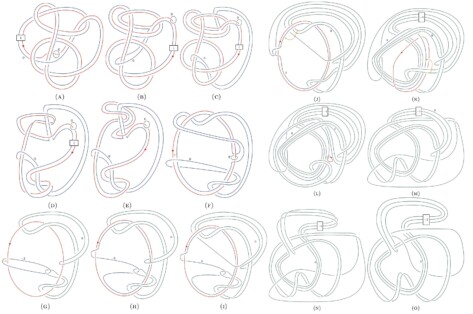
That was until Lisa Piccirillo, Ph.D., then a graduate student at The University of Texas at Austin, determined it was not.
According to a profile in Quanta Magazine, Dr. Piccirillo learned about the Conway knot problem during a lecture by Shelly Harvey, Ph.D., of Rice University. Dr. Piccirillo was attending a mathematics conference on low-dimensional topology and geometry in the summer of 2018 at UT Austin.
This lecture, however, sparked something more. It prompted Dr. Piccirillo to explore this Conway knot, the mathematical problem that has stumped others for years. Topologists use mathematical tools called invariants to try to determine sliceness, but for whatever reason, those tools could not prove the prevailing belief that the Conway knot was not slice. Perhaps, however, scholars and mathematicians had decided to leave well enough alone. Perhaps they resolved themselves that it could not be solved. After all, this knot is a sculpture design that adorns a gate at the Isaac Newton Institute for Mathematical Sciences at the University of Cambridge.
Dr. Piccirillo was not deterred.
“I was motivated to think about it because it was so absurd that it was unknown. In general, for a small knot like that, mathematicians are quite good at determining sliceness,” she said. “I didn’t know anything about the history of the problem; I just thought the Conway knot shouldn’t really be so much harder than any other.”
She solved the problem less than a week later, using techniques and tools she learned in her related work and from her award-winning dissertation. Titled “Knot Traces and the Slice Genus,” it won UT Austin’s 2019 Michael H. Granof Award — the university’s top dissertation and graduate student award. Her dissertation examines knots and four-dimensional spaces and resolves two well-known mathematical problems: one from the Kirby List of Problems; the other first presented by Conway.
“When I was just starting research, I learned about the problem from the Kirby list and found it interesting but presumably hard,” she explained to The University of Texas at Austin College of Natural Sciences news service. “Then, a few months later, someone solved a smaller case of it. That was very exciting and made me think that maybe the big problem was approachable with modern tools. That was pretty bold, but I enjoyed working on the problem, so I was able to keep at it and eventually something worked,” she said. “The Conway problem was serendipitous; someone mentioned the problem in a talk, and I realized immediately that it should be approachable using the tools I study.”
Her findings were published in March in the Annals of Mathematics, a bimonthly mathematical journal produced by Princeton and the Institute for Advanced Study.
While the typical overhand knot — the kind you tie at the end of a thread — sees the string cross over itself three times, the Conway knot has 11 crossings. What Dr. Conway wanted to know is whether his knot can be formed by cutting a slice out of a more complex four-dimensional knot — or, as mathematicians asked, is it “slice”?
Dr. Piccirillo’s chief interests are in the topology and geometry of four-dimensional spaces. She described 4D space in this way in a UT Austin news story:
“If an ant living on the earth would like to leave an island without touching the water, it is going to have a hard time. Because on the 2-D surface of the Earth, the water completely surrounds the island. But, if the ant builds a bridge (which rises up, into a third dimension, above the water), then suddenly it has an option to leave the island. We naturally think about 3-D space all of the time. Studying 4-D space is fun because, just as the ant can leave the island once it’s allowed to go up, in four dimensions more things are possible.”
Dr. Piccirillo said she’s always been drawn to spatial reasoning because of the creativity it requires and because it challenges her to think carefully about objects that she cannot draw. “I think math is always really creative,” she said. “I don’t imagine I am much more so than any other mathematician. Certainly, the style of math I do requires a lot of subtle visualization, and I like problems where I can try to cook up an object that satisfies many seemingly contradictory constraints.” It is also what helped her “think outside the knot’’ to settle the Conway problem and further her own research in three- and four-manifolds and knot concordance.
Her discovery, its placement in the Annals of Mathematics, and several talks led to her securing a tenure-track position at the Massachusetts Institute of Technology, where she is an assistant professor. She earned a Ph.D. in 2019 from UT Austin, supervised by John Luecke, Ph.D., and was a National Science Foundation postdoctoral fellow at Brandeis University under Danny Ruberman, Ph.D. Postdoc positions are typically three to four years long, but her solution to the Conway knot drew widespread interest and the job offer at MIT.
Mentors and role models matter
Dr. Piccirillo, who grew up in rural Greenwood, Maine, describes herself as an overachiever. She was active in her church, participated in drama, and played in the band. Her mother taught middle school math, and while Dr. Piccirillo did well in the subject, she did not necessarily envision herself becoming a mathematician.
When she enrolled at Boston College in 2009, her initial interest was in theater. Yet after completing a calculus course taught by a woman professor and being encouraged to take more math courses, Dr. Piccirillo was hooked. She completed a B.S. in mathematics in 2013. She chose to attend UT Austin, known for its exemplary graduate program in mathematics and its reputation for supporting female math students. It also ranks eighth in the country in topology, the field she wanted to pursue.
UT Austin did not disappoint. During her six years there, she experienced strong mentorship and a supportive research community, which overshadowed any doubts others may have had toward her. Dr. Piccirillo credits the topology group for its assistance and guidance in her research as well as UT Austin’s attention to sponsoring seminars with a strong commitment to quality exposition. She also singled out Dr. Luecke, her graduate advisor, and UT Austin mathematics professor Cameron Gordon, Ph.D., for their patience and leadership as she developed her skills and confidence. In fact, Dr. Gordon urged her to submit an abstract about the “Conway knot is not slice” discovery to the Annals.
Although Dr. Piccirillo faced some skepticism, she said she felt encouraged and welcomed as a female mathematician while at UT Austin. One does not have to be “smart” to be a successful mathematician, she said in a Boston Globe story. The idea that one has to be a genius or a math prodigy or even brilliant did not necessarily apply to her; rather, a keen interest, dedication to learning, coupled with robust mentorship, can go a long way.
Now at MIT, Dr. Piccirillo has joined an institution that has recognized the underrepresentation of women in STEM fields, particularly math, and is working to develop a more inclusive and supportive environment through such campus-based organizations as Women in Mathematics, the MIT Society of Women Engineers, and Women@MIT, among others.
Once normal campus operations resume in light of the global pandemic, Dr. Piccirillo plans to get to know the students, the mathematics department, and doing whatever she can to broaden the mathematics community and upend the myth of the math prodigy.